El post anterior era un juego basado en las estadísticas del INE sobre la distribución por provincias de los apellidos. Pensé que hay apellidos que son provincias, y (ya se sabe el vicio que tiene uno con la autorreferencia), se me ocurrió buscar la distribución por provincias de esos apellidos-provincia. Ver, por ejemplo, donde caen los Sevilla, Zaragoza, Lugo o Soria…
Los resultados son bien curiosos. Primero, no esperaba que casi todas las provincias tuvieran su apellido. Nunca había oído de nadie que se llamara Badajoz o Ciudad Real, pero estos apellidos, aunque poco frecuentes, existen. No hay sin embargo ningún Sr. o Sra. Guipúzcoa o Cantabria (lo que indica seguramente que no son nombres geográficos muy antiguos).
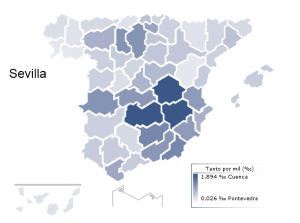
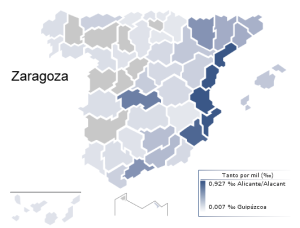
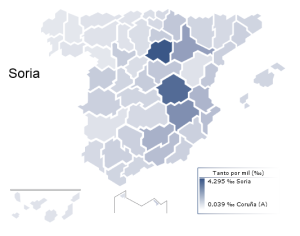
Pero aceptado que (casi) para cada provincia hay un apellido, ¿cómo es la correspondencia entre provincias y apellidos?¿Sevilla se limita a Sevilla o se desparrama por toda España? Pues en general, un determinado apellido-provincia es escaso en la provincia homónima. En Lugo, por ejemplo, sólo viven 13 de los 2701 Lugos que hay en España, mientras que son sorprendentemente abundantes en Santa Cruz de Tenerife (nada menos que 864). Hay sin embargo excepciones: la frecuencia relativa de los Soria tiene un máximo, precisamente, en Soria (no así la de los Soriano, cuyo máximo está en Teruel).
Todos estos datos se pueden reunir en una tabla: provincias en filas y apellidos en columnas. Si tuviera tiempo lo haría, porque con esa tabla se puede jugar a muchas cosas.
Por ejemplo, podemos imaginar una hipotético apellido puro: el que estaría limitado sólo a su provincia homónima. Sería lo que pasaría si todos los Sevilla vivieran en Sevilla. Para un apellido puro, la correspondiente columna de la tabla sólo tendría un elemento distinto de cero: el de la diagonal.
En la realidad no hay apellidos puros; al contrario, los elementos más grandes suelen estar fuera de la diagonal, como hemos visto. Pero ahora imaginemos un pasado prístino en el que todos los Sevilla vivieran en Sevilla, como Dios manda (y todos los Zaragoza en Zaragoza, etc). Podemos conjeturar que el actual estado de impureza en los apellidos es la consecuencia del desparramamiento por el mapa de las poblaciones puras iniciales. Cada columna de nuestra tabla nos indica como se ha dispersado la correspondiente población inicial, hasta llegar al actual estado de desorden.
Pero ¿de verdad es tan desordenado el estado actual? Podemos argumentar que sólo nos parece desordenado porque seguimos empeñándonos en usar las provincias originales. De hecho, se pueden definir unas nuevas provincias de manera que la tabla vuelva a ser diagonal. Lo que pasa es que cada una de estas nuevas provincias tiene que ser una mezcla: una combinación lineal de las originales. En otras palabras: teníamos provincias puras y apellidos impuros, y ahora con las provincias-mezcla tenemos apellidos puros y provincias impuras. Son dos maneras de ver la misma situación.
* * *
Como seguramente no se entienda nada, vamos a verlo con un ejemplo. Supongamos que no hay más que dos provincias (y apellidos), A y B. Sean Ávila y Burgos. La tabla de datos es la siguiente:
Los datos están en cientos de personas, así que la primera fila significa que en Ávila hay 44 personas con el apellido Ávila y 82 con el apellido Burgos, y la segunda que en Burgos hay 104 personas con el apellido Ávila y 421 con el apellido Burgos.
Ahora imaginemos una provincia-mezcla que tenga un 30% de Ávila y un 70% de Burgos; la llamamos P0, y escribiremos P0=(0.30,0.70). El número de apellidos Ávila y Burgos que tendría P0 sería:
Pero no tenemos porqué restringirnos a combinaciones lineales en las que los coeficientes sumen 1, como P0=(0.30, 0.70), ni siquiera a números positivos. Supongamos dos nuevas combinaciones lineales, que vamos a llamar P1=(4.21, -0.82) y P2=(-1.04, 0.44). Los correspondientes números de apellidos serían:
Para este nuevo juego de provincias impuras {P1,P2}, los apellidos Ávila y Burgos son puros. Por el contrario, para las provincias originales puras, las apellidos Ávila y Burgos son impuros.
* * *
Los lectores versados en matemáticas ya se habrán dado cuenta de lo que hemos hecho. Lo que hemos llamado tablas es lo que en matemáticas se llama matrices. Y para construir las provincias-mezcla que hacen que los nombres sean puros, simplemente hemos calculado la matriz inversa:
de modo que el producto sea la matriz identidad:
O sea, que no era en el fondo más que álgebra lineal. Estamos tratando los apellidos y las provincias como vectores, y su pureza o impureza depende de la base que elijamos en el espacio vectorial.
Pero ¿qué sentido tiene todo este juego?¿Eso de las provincias impuras y del álgebra lineal con los apellidos no es, con perdón, la paja mental de un friki?
Bueno, quizá no. Lo que yo he llamado provincias impuras viene a ser lo que se llama en física superposición cuántica. Lo del gato de Schrödinger y todo eso. Una de las pocas cosas que sabemos a ciencia cierta de la realidad última de la materia, de los átomos y las partículas elementales, es que se comportan como vectores y se puede operar con ellos siguiendo las reglas del álgebra lineal. Algo que vio por primera vez Heisenberg y formalizaron luego Dirac y von Neumann. Hace de ello ya más de 80 años, pero todavía seguimos sin entender que el mundo no está hecho de ladrillos, sino de fantasmales provincias impuras.


¡Cartagena, Provincia! ¡Viva Cartagena!
Sin meterme en los asuntos matemáticos, creo que puedo aportar un granito de arena.
Este país, especialmente la península, tuvo un proceso repoblador, sin este proceso mal podrían haberte mantenido las conquistas de territorios, que duró unos mil años. Sí, el proceso repoblador no acabó ni en siglo XIII ni en 1492. No hay que olvidar que una buena porción de habitantes de algunas zonas muy concretas fueron expulsados en 1609, y otros desplazados antes. No me meto con esto ni lo juzgo. Los que en aquel momento lo hicieron, tomaron la decisión porque lo creyeron oportuno para las circunstancias de su presente que no son las del nuestro.
Con este rollo quiero llegar a una parte de la entrada: es normal que los apellidos originados en una zona no sean precisamente abundantes en ella, por ejemplo, los Lugo en Lugo. El proceso de asentamiento de los apellidos tardó siglos, y una de las maneras de «tener» un apellido aparte del antiquísimo y prerromano patronímico sufijo «ez» o «is», hijo de, fue precisamente unir el origen geográfico al nombre. En la zona donde vivo y soy originaria hay una buena cantidad de apellidos Pallarés, de los valles pirenaicos de Pallars Jussà y Pallars Sobirà, y Ripollés, de Ripoll. «Soriano» también hay unos cuantos y «Navarro»…, sólo hay que tener unas pocas nociones de Historia…, que no es la disciplina más popular actualmente. 🙂
Bueno, Ripollés también es el nombre de la comarca cuya capital es Ripoll, no lo olvidemos XD. Lo curioso es que cuando he ido ahí (amigos de mis padres viven allí), nunca hemos hablado de Ripoll, sino de Ripollés. Y por tanto, ya no se si he ido a lo que es la capital o a alguna de las aldeas XD.
Dios, interesante es cuanto menos… pero tendré que leérmelo nuevamente para entenderlo en toda su plenitud.
Por otro lado es muy interesante eso de que hagas divulgación científica en forma de juegos, se hace amena, aunque es tan rebuscada que podría echar a mucha gente para atrás.
Y a los reduccionistas irredentos eso de que el mundo no esté fabricado con ladrillos bien palpables, lógicos y definidos les trae de cabeza. Reconozco que a mí todo esto de la física cuántica me supera. Parece que a los físicos también 🙂 lo cual ayuda un poco a mi maltrecha vanidad por aquello del mal de muchos. Pero, aun así, he de decir que me encanta todo lo que me supera. Gracias, señor Pseudópodo, por engrasar los engranajes de este cocamen mío, que anda hoy de reposo dominguero. Un abrazo… cuántico.
» Pero ahora imaginemos un pasado prístino en el que todos los Sevilla vivieran en Sevilla, como Dios manda (y todos los Zaragoza en Zaragoza, etc) »
Pues si mal no lo entiendo el apellido puro debería de no estar nunca en su ciudad homónima, dado que su origen, se supone, consiste en un mote identificativo de los «recién llegados» que en su momento se bautizaban globalmente según el origen, al igual que en la mila nos poníamos como alias la ciudad de origen, y te ibas con el Sevilla de cervezas.
Si, lo se, ya son ganas…
🙂
Este no llega a los 100 comentarios. Si el ejemplo de la provincia pura hubiese sido Cataluña, entonces quizá sí. Porque Cataluña es cuántica, lo dijo Dalí, creo.
(Pido disculpas de antemano por no poner tildes. Escribo desde un ordenador prestado)
Yo diria que la abundancia de Lugos en la provincia de Santa Cruz de Tenerife no es sorprendente si se tiene en cuenta que el conquistador de Tenerife y La Palma fue Alonso Fernandez de Lugo, o simplemente Alonso de Lugo, nacido en Sanlucar pero de familia originaria de Lugo, de la Casa de Lugo de toda la vida (o por lo menos de tiempos de la reconquista). Supongo que el apellido se extendio, no tanto por sus descendientes (que, a proposito, lo acabaron envenenando), sino porque habia mucha gente a la que bautizar y el era el duen~o de todo. Lo mismo que en la provincia de Las Palmas abundan los Bethancourt (o Betancor y similares) por Jean de Bethancourt, el primero en ocupar Lanzarote y Fuerteventura.
En definitiva, que la historia ha hecho que haya apellidos-provincia con mucho mas peso que otros. No se si esto encaja en tu matriz cuantica, que me ha resultado muy interesante en cualquier caso.
¡¡Cristina!! ¿pero qué clase de amigo es ese que te presta un ordenador sin derecho a usar la tilde? 😉
Pues un amigo ‘atildado’ 🙂
Releeré el post otro día pero de momento las matrices me han echado para atrás porque no las manejo.
por esa razón, en una primera lectura me parece que casi es más fácil entender el asunto que pretende divulgar hablando de partículas, vectores, ondas, campos de fuerza o lo que sea que seguir la historia de las provincias impuras.
Iba a precisar una cuestión onomástica pero Hesperetusa se me adelantó. Efectivamente, los apellidos surgen como sistemática onomástica a partir del XVII, El parámetro más usado fue diferenciar… A un natural de Lugo, resulta inútil identificarlo como Carlos de Lugo en Lugo, la cosa cambia en Soria, donde ser Carlos de Lugo, te distingue del resto de habitantes.
Y tú te me has adelantado a mí. je je
También a mí se me ocurrió lo mismo que a Hesperetusa, que no tiene que ver con el objetivo del post, pero me parece intersante.
No tiene sentido que un apellido como Sevilla naciera en Sevilla (qué sentido tendría distinguir así a alguien en la propia Sevilla), lo lógico es que llamaran así a forasteros en otro lugares que venían de allí. Y es probable que los Sevilla que viven en Sevilla son descendientes que volvieron, lo cual tampoco parece disparatado porque podían tener lazos familiares…
Don Loia, en algunas ciudades existía la costumbre de poner como apellido el nombre de la ciudad a los nacidos sin apellido reconocido, como huérfanos, hijos de mujeres solteras, etc.
pues no lo sabía
Otra vía por la que entran las ciudades en los apellidos es por la judaizante.
Una cosa que siempre me ha parecido curiosa: ¿esos «científicos que ven la materia como bolitas» de qué ramas suelen ser?. Se me ocurre que por analogía, pueden ser química (por la visión de moléculas como bolitas, aunque alguien me corrija) y biología (por que su manera de investigar presupone un determinismo que la física no hace). Pero no lo se.
Dr.J, Murcia gana a Cartagena por 9500 a 2022, pero con mucho menos se han hecho provincias….todas las de Albacete para abajo…
Hesperetusa, David, avatariamode y loiayirga señalan algo que ya habíamos dicho josele y yo en los comentarios al post anterior (“en Cataluña no tiene sentido llamar a alguien Catalán, en Teruel sí…” decía yo, por ejemplo), aunque se agradecen las precisiones… Lo que no sabía era lo que han señalado avatariamode y Alejo Urzass: que los apellidos-provincia (o -ciudad) pueden ser de origen judío (lo he comprobado en esta página, por cierto) o de huérfanos, hijos naturales, etc…
Cristina, gracias por aclarar el misterio de los Lugos canarios… Hay muchos “endemismos canarios” en los apellidos: por ejemplo Santana, Cabrera, Rivero… y luego hay casos curiosos como Suárez, que está muy extendio en Asturias y Las Palmas. Seguro que hay una explicación histórica; en realidad, estos datos de apellidos son como el registro fósil, y se podría aprender muchísimo de ellos. Si nuestros historiadores tuvieran idea de estadística, o si en España se comunicaran los universitarios de facultades distintas, ya se habrían puesto en marcha proyectos de investigación para explotar este registro.
Bloodykefka, yo creo que efectivamente químicos y biólogos tienden a ver la materia como bolitas, pero no te creas, los propios físicos tienden también a hacerlo. La cuántica y lo que significa casi nadie la tiene interiorizada; incluso quienes trabajan en, por ejemplo, estado sólido, que no se pueden entender sin cuántica, yo diría que rara vez piensan en las “rarezas” que la cuántica nos ha enseñado sobre la materia.
loiayirga, en realidad, este post es si le lee con atención una explicación de lo que son las matrices y de por qué se multiplican como se multiplican. Pero tampoco es que pretendiera divulgar nada, en realidad,el interés que tiene este post, yo creo, es como ejemplo de cómo puedes pensar y ver las cosas desde ángulos nuevos gracias a la física. Por supuesto, es un juego, no pretendía que en realidad hubiera provincias prístinas en el pasado, pero lo que hago aquí es un modelo que es natural para un físico. De hecho, la idea de que las poblaciones “se desparraman” por el mapa esta inspirada (en mi caso por lo menos) en la idea de que cuando se usa un aparato para medir, por ejemplo, un espectro, el aparato no tiene una resolución infinitamente buena y hace que los datos “se desparramen” por las posiciones vecinas del eje de longitudes de onda… Luego, me hizo gracia que la idea de las “provincias impuras” era análoga a la de la superposición cuántica, y por eso me animé a escribir el post… que por cierto me ha costado un montón, entre las ecuaciones y las vueltas que le di a la analogía (para matemáticos: lo primero en que pensé para conseguir apellidos puros fue en diagonalizar la matriz, y tardé en darme cuenta de que no se trataba de eso)
Ana, efectivamente, el reduccionismo del «ladrillo» es un vicio tan malo (y tan tentador) en ciencia como en economía 😉 Yo vaticino que también en ciencia el ladrillo va a entrar en crisis pronto (pero debía haber entrado hace muchos años y ahí lo tienes…)
Ah, Alejo: Dalí sabía más física de la que parecía… pero de si puede definirse una Cataluña (por ejemplo) pura, o al menos de algo parecido, quería hablar en otro post, a ver cuando saco un rato.
Yo iba a comentar también que los apellidos con nombres de ciudades solían ponerse por los curas a niños abandonados.
Se ponía el nombre del pueblo o de la parroquia. De ahí vienen muchos apellidos como San Juan.
En realidad los «nombres de provincia» como apellidos son nombres de pueblos. Por eso hay mucha gente con el apellido Bilbao pero no el apellido Vizcaya, ni Guipúzcoa.
(Don Josu, le he corregido el enlace, que no funcionaba) Y sí, es verdad que los apellidos-provincia son en realidad apellidos-pueblos o apellidos-región… sólo que me venía bien para convertirlo en un juego autorreferencial. Sí tenía idea de que los apellidos como San Juan, Sampedro, etc, eran frecuentemente de niños abandonados (expósitos), lo que no sabía era que el nombre viniera de la parroquia.
Para pseudópodo: bueno, también hay que tener en cuenta que es una cuestión metodológica, y que la cuántica es dificil de interiorizar. A mi me cuesta, y más que interiorizarla, la uso para «abrir mi mente» y cuestionar mi entendimiento. Lo que pasa es que tenía curiosidad de ver a quienes te referías, puesto que la química y la biología suele hacer esas presunciones, y bien debe hacerlas, al fin y al cabo se hacen más entendibles, otra cosa es que las saques de su ambito para hacer filosofía con ellas.
PD: Vaya, con la aparición de malaprensa, veo que este blog tiene parte de la flor y nata de la blogosfera.
Cierto que es difícil de interiorizar y en realidad no pasa nada… mientras no se haga filosofía, como bien dices. Entonces suele caerse en lo que podíamos llamar «cientifismo del ladrillo», que es, como decía yo a Ana arriba, tan peligroso como la economía del ladrillo.
(Y bueno: no parte, ¡la flor y nata entera de la blogosfera se asoma por aquí! 😎 )
Yo no es por la peligrosidad, es que luego si se tiene cierta pretensión «general», quizás se esten partiendo de unos presupuestos tan particulares que se pueden cuestionar, incluso para defender lo mismo.
No sé si se lo he leído a Pseudópodo en este blog o me lo explicó otro físico, pero a mí si tengo que dejar de pensar en un mundo de partículas mejor que lo de las matrices me resulta más fácil (y más visual) pensar en el símil de la piel de un tambor. Cada “objeto” colocado sobre ella produce un hundimiento que se nota en toda la superficie del tambor. De ese modo cada objeto puede ser visto como un cúmulo de fuerzas que están representadas en el símil por las inclinaciones que causan sobre la piel.
Para hacernos idea de lo que es la realidad tenemos que prescindir de los objetos e imaginarla como esa piel tensa cruzada por mil fuerzas diferentes (hundimientos aquí y allá que tiran unos de otros y todos se interrelacionan).
Wittgenstein fue el que habló de los problemas filosóficos que crea el lenguaje. La filosofía tiene que enseñar a la mosca a salir de la botella en la que se metió. Un lenguaje donde lo importante son los sustantivos (palabras inamovibles) nos hace pensar que las cosas son eso: cosas con identidad estable. Creemos que el mundo está formado por cosas que actúan o sobre las que se actúa. Quizás por el lenguaje (mi nombre no ha cambiado en cincuenta y tantos años y me hace creer que soy el mismo que fui) nos sentimos mucho más estables de lo que somos. Un lenguaje de sustantivos nos llevó a una metafísica de la sustancia. No sé si esas fuerzas o vectores o campos de fuerza o lo que sea podrían estar representados mejor por los verbos. En todo caso, cualquier concepto, aunque sea el concepto de una acción, al ser fijo y permanente nos engaña con respecto a una realidad que es más dinámica y fluida de lo que queremos creer.
La distinción entre “objeto” y “sujeto”, por ejemplo, al referirnos a ellos con dos palabras estables nos engaña con respecto a su ser. En realidad no hay más que una única realidad (la vida la llamaba Ortega, aunque creo que el vocablo sólo nos puede confundir más) en la que se encuentra la conciencia y el mundo, pero no como dos cosas hechas que coexisten sino como si fueran los conceptos de arriba y abajo que son correlativos y no pueden existir uno sin otro. Husserl fue el que vio ese carácter intencional de la conciencia. La conciencia solo puede ser conciencia de algo, tiende hacia algo. Y ese carácter tensional (quizás se pueda decir así) no es fácil de comprender porque al pensarla con una palabra “conciencia” la convertimos en cosa, en partícula, en lugar de verla como energía referida a algo que a su vez no es tampoco una cosa sino aquello a lo que la conciencia ser refiere.
Creo que alguna vez leí que la conciencia podía pensarse como una explosión. Digamos que únicamente de un modo intelectual podemos diferenciar sujeto y objeto, lo que existe es ese lugar a medio camino donde se encuentra la conciencia con el mundo. Aunque a su vez la palabra encuentro sea engañosa porque remite a dos realidades previas que se conectan. Debíamos pensarlo al revés. Es una realidad en que nosotros nos empeñamos en diferenciar dos.
YA me perdí.
🙂
loayirga. Felicidades, Aunque soy filósofo y se supone que algunas cosas ya las tendría que saber,, usted me ha aclarado algunos conceptos. De todas maneras me lo vuelvo a leer. Iba a comentar que la analogía elegida por Psuedopodo, es elegante, bonita, pero algo confundente
Reconozco que el tema de las matrices se me escapa un poco aunque (y he aquí lo grave) las di en COU y en la Universidad. Las recuerdo emparentadas con los espacios vectoriales… y siento que aquello era lo más de lo más. (Por cierto, qué shock cuando me dijeron que había espacios vectoriales de más de 3 dimensiones).En su tiempo incluso llegué a entender todo eso (o eso me creía :)) La idea que me quedó es que las matrices son una herramienta poderosísima para manipular aspectos de la realidad, pero a la vez algo tan abstracto y «pesado» para mi cabeza que…mejor relegar a las máquinas.
Enlazando con el tema de la física cuántica y sobre lo que comentáis de lo difícil que puede ser de interiorizar. Me pregunto, ¿puede alguien que no ha estudiado a fondo la mecánica cuántica en toda su base matemática, decir que la entiende? ¿Puede alguien, aunque no sea «de ciencias» entender sus presupuestos básicos? ¿Sirven las metáforas tipo «gato de Schrödinger»?
Cuando estudiaba las leyes de Newton podía ver su aplicación directa al jugar un partido de fútbol o al coger un plato de sopa. Había un equilibrio entre teoría y práctica. Con la mecánica cuántica, me da la sensación de que aunque conozca bien la teoría, jamás la integraré con la práctica (a menos que trabajara en el CERN… y ni así). Sí, puedo fijarme en los móviles, el GPS… que utilizan tecnología basada en la mecánica cuántica, pero sigue estando oculto para mí a nivel intuitivo. Especialmente aquellos aspectos más paradójicos.Ya no es eso de estar en un coche y al frenar de golpe e irte hacia adelante pensar, ¡toma, la ley de la inercia!
No sé, igual llegará el día que todo esto que a muchos nos parece tan raro (y maravilloso) de la física cuántica, sea «interiorizado» por la gran mayoría. O igual no, y siempre será algo elitista (en el mejor sentido de la palabra).
En realidad, supongo que antes de la cuántica ya habían muchas cosas que se escapaban de lo «comprensible» para la mayoría, como el electromagnetismo…
Por cierto, loiayirga, qué interesante tu último post no-dualista.
Triglifo, no me extraña que te pasara eso con las matrices. En realidad, yo sólo he empezado a disfrutar de ellas (se podría incluso decir así) cuando las he tenido que usar en problemas de física que me han surgido en la investigación. Pero la idea básica es que aparecen inevitablemente cuando trabajas con espacios vectoriales, y los espacios vectoriales aparecen inevitablemente cuando trabajas con cosas como fuerzas, velocidades… Intuitivamente, con “flechitas”, pero lo decisivo, cuando se estudia el asunto, no es que sean “flechitas” sino que obedezcan al principio de superposición: por ejemplo, para saber cuál es la fuerza total sobre un objeto, hay que superponer (sumar al modo de los vectores) todas las fuerzas que actúan sobre él, y luego nos podemos olvidar de las fuerzas individuales. Y a la inversa: podemos descomponer en componentes la fuerza total (o la velocidad) y tratar cada una por separado. Ese fue un gran descubrimiento de Galileo, y por eso pudo explicar por ejemplo el tiro parabólico, que nadie antes había entendido.
En el ejemplo de las provincias, trato cada apellido como si fuera un vector, y sus nº de personas en cada provincia como sus componentes (de manera que si hay 50 provincias, ¡el apellido es un vector de 50 dimensiones! ) El valor numérico de las componentes depende de la “base” que elijamos (en 3-d la más habitual son los tres vectores unitarios, uno según cada eje xyz; aquí, en 50-d, la base natural son los “apellidos puros”, y lo que hago es cambiar de esa base a otra que es la de los “apellidos-provincia” que teníamos de partida).
Sobre entender la MQ, hay una cita célebre de Feynman: “Si usted piensa que entiende a la mecánica cuántica… entonces es que usted no entiende la mecánica cuántica”, y muchos otros dijeron cosas parecidas. En realidad estos problemas para entenderla surgen de que nos empeñamos en usar conceptos familiares, macroscópicos, para “cosas” que no funcionan así en absoluto. Matemáticamente no es tan difícil de entender, tiene una formulación muy elegante, y de hecho en algunos sentidos es más sencilla que la de la mecánica clásica (por ejemplo, todas las ecuaciones son lineales). Sin esos conceptos matemáticos yo creo que realmente poco podemos entender, y Feynman y compañía tienen razón.
De todos modos, creo tienes mucha razón con eso de que “antes de la cuántica ya habían muchas cosas que se escapaban de lo “comprensible” para la mayoría”. El propio electromagnetismo que dices es un ejemplo, pero incluso nociones más elementales, si las empezamos a analizar con actitud filosófica, son muy difíciles. Lo que pasa es que son nociones que están menos en desacuerdo con nuestro “sentido común” y por eso nos las tragamos sin verles los problemas (por ejemplo: el espacio absoluto de Newton o la acción a distancia).
loiayirga, lo de que para hacernos idea de lo que es la realidad tenemos que prescindir de los objetos e imaginarla como esa piel tensa cruzada por mil fuerzas diferentes estoy seguro de que (te) lo he dicho yo 🙂 pero te autorizo de muy buen grado a que difundas esas ideas tan queridas por mí. La metáfora del tambor es seguramente la mejor para entender lo que es un campo, y efectivamente la cuántica ve todo como campos (y esos campos obedecen al principio de superposición, con lo que volvemos a los espacios vectoriales).
Me ha gustado mucho, además, tu enfoque filosófico (¿por qué no un post en tu blog, sin el “Ya me perdí” al final 😉 ) . Lo de “Un lenguaje de sustantivos nos llevó a una metafísica de la sustancia” está muy bien, aunque quizá tenemos esa predisposición a ver sustancias y era inevitable que desarrolláramos ese lenguaje (el problema del huevo y la gallina). Creo que había un cuento de Borges sobre una tribu que tenía un lenguaje sólo hecho de verbos, pero no sé si algún lenguaje humano real escapa a la estructura sujeto+predicado…
La verdad es que yo de momento soy más simple: pues aunque soy consciente del sentido de no imaginarse la realidad como ladrillos, yo lo entiendo más en un estilo de «significado» en el hecho de que el mundo es más «raro de lo que parece» (el determinismo que no supone la física y por el que se debate). Si tuviera que abstraerme, yo me imagino la materia así.
Si, sigue siendo bolitas… solo que para mi esas bolitas que se superponen son en realidad los estados de una misma partícula «vistos a la vez» y nuestros ojos simplemente podría ver unos u otros.
Ya se que no es muy buena, pero no soy físico.